|
Conceptos fundamentales explicados
Actitud
mítica
Explicación de la filosofía de los principales pensadores, resúmenes, ejercicios...
Breve definición de los términos y conceptos filosóficos más importantes en la Historia de la Filosofía Occidental
Explicación de los principales conceptos, tesis y escuelas en el área de la Psicología
|
|
|
Muerte de Sócrates |
|
|
|
|
Aporías de zenón O paradojas de Zenón. Argumentos presentados por Zenón de Elea para demostrar el carácter absurdo de la creencia en el movimiento y la multiplicidad y de ese modo defender las tesis de su maestro Parménides.
Aporía: del griego aporía (“paso impracticable”, “camino sin salida”). Con
el término aporía nos referimos a la situación que se crea cuando un
problema carece de solución o da lugar a conclusiones absurdas. Argumento de Aquiles y la tortuga |
|
|
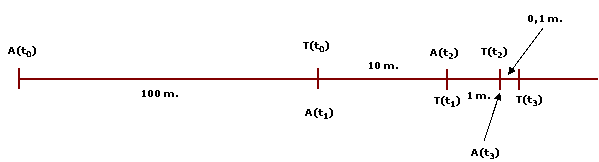
A: Aquiles T: Tortuga t0, t1, t2, t3, ... : tiempo 0 o salida, tiempo 1, tiempo 2, tiempo 3, ... |
|
El más rápido de los hombres, Aquiles, no podrá alcanzar nunca al más lento
de los animales, la tortuga, si en una carrera se da a ésta una ventaja
inicial: supongamos que Aquiles le da a la tortuga una ventaja de 100
metros. Para facilitar la comprensión pongamos que Aquiles sólo corre diez
veces más rápido que la tortuga; en el t0 Aquiles está en la salida y la
tortuga a 100 metros; en el t1 (pongamos que 15 segundos) Aquiles recorre
100 metros y la tortuga 10; en el t2 (que es 1/10 de t1 = 1,5 segundos)
Aquiles llega al punto en el que antes estaba la tortuga y ésta recorre 1
metro; en el t3 (que es 1/10 de t2 = 0,15 segundos) Aquiles recorre este
metro pero la tortuga recorre un decímetro; y así sucesivamente. La
estrategia del argumento consiste en considerar los tiempos cada vez más
pequeños, precisamente en la proporción en que Aquiles le aventaja a la
Tortuga en velocidad (1/10), de este modo, aunque en tiempos y en distancias
cada vez más pequeñas (una décima parte en cada tiempo considerado) Aquiles
nunca alcanzará a la Tortuga, y así la tortuga irá llevando la ventaja hasta
espacios infinitamente pequeños. Recorrer un número infinito de puntos
parece suponer, por tanto, recorrer un tiempo infinito. Aquiles no podrá
alcanzar jamás a la tortuga aún cuando, evidentemente, se vaya aproximando
infinitamente a ella.
|
|
Ver “paradojas de Zenón”.
|
|
|
|
||||
|
© Javier Echegoyen Olleta |
||||





